Project Goal

Cryo-Electron Microscopy (cryo-EM) is a technique for obtaining 3D structures of molecules from an electron microscope. Its advantages over x-ray crystallography are reduced sample requirements and no need for crystallization. The central problem in "single-particle" cryo-EM is the problem of reconstructing a 3D shape from 2D projections of unknown orientations. It's the unknown orientations that makes this problem new and difficult, compared to say medical computed tomography. A frequent occurrence is convergence to an incorrect local optimum.

---

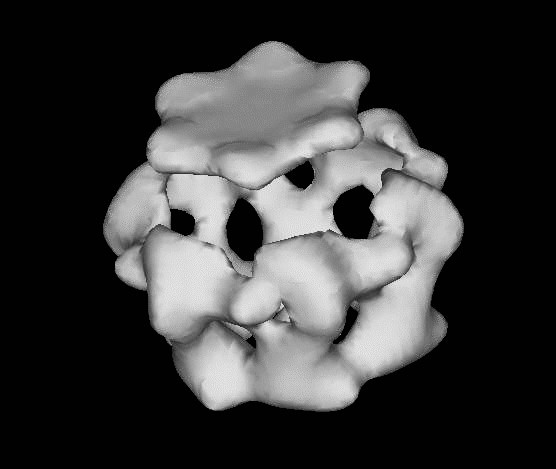
Figure 1: Correct or bogus?

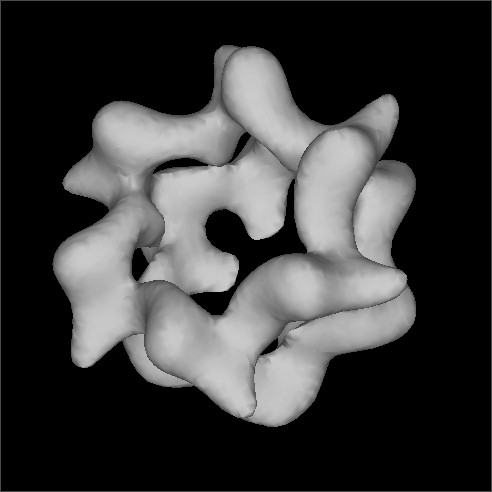
Figure 2: Correct or bogus?

---

See the figures-- one is correct and one is bogus-- can you tell which is which?

Project Scope

This project involves interfacing with Dr. Marshall Bern of PARC. Most of the project will involve synthetic data, but we have one problematic real data set, and we can get more if we like. We have already done a similar project for an analogous 2D reconstruction problem, but we now think that the 2D problem does not capture all the difficulties of the real 3D problem.

Tasks

The project will be accomplished through the following tasks.

• Task 1: Program a simple 3D reconstructor. This should not be too hard, assuming we use MatLab or any other package that includes 2D and 3D FFTs. The FFT of a projection is a central slice in the frequency domain; we just average each slice into the grid of voxels and then back-transform.

• Task 2: Create synthetic problematic data sets, that is, sets with incorrect local optima that are hard to avoid. We need a way to create 3D geometry and make arbitrary projections with noise added. Again existing software could be helpful.

• Task 3: Experiment with the following ideas for avoiding local minima: Soft assignment of orientations (standard cryo-EM software uses hard assignments), Multiple initial models (standard software makes a best guess), Multi-resolution reconstructions (start with a very coarse reconstruction), Simulated annealing (bounce around the space of reconstructions).

Project Status

Pierre-Alexandre Pont, Mathieu Bredif, and Uygar Sumbul

Point of Contact

Daniel Russakoff

Midterm Report

submitted

Final Report

submitted